This post’s topic: Joukowsky (wing, transformation, and how they are shown with equations (tried not to be very complicated)
What is a Joukowsky wing?
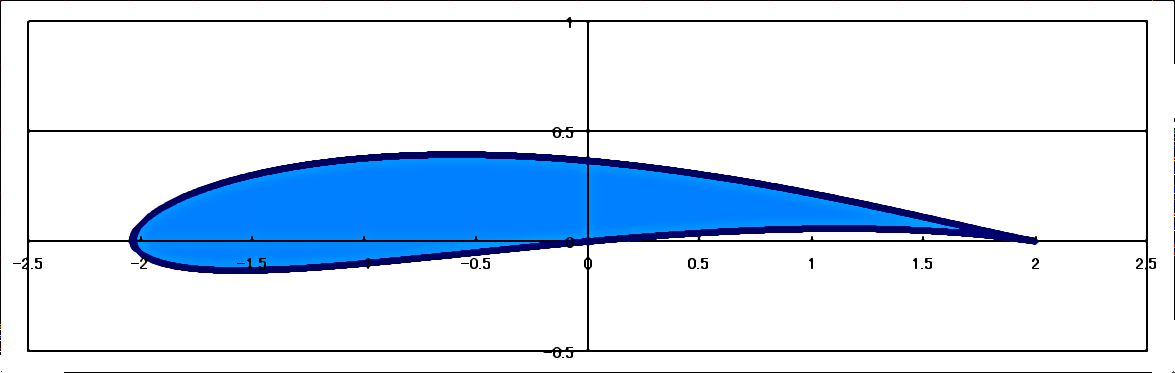
Basically, it is “a mapping transformation from circular to airfoil by the Joukowski transformation“
picture of a Joukowski Airfoil (wikimedia commons)
Then what is a Joukouwski Transformation?
It means “To convert a point \(ζ)\ (eq.1) in the complex plane to a point\(z)\ (eq.2) in the real plane.”
\(ζ=(ξ+ iη)\)・・・(eq.1)
\(z=(=x+iy)\)・・・(eq.2)
This conversion can be shown with (eq.3). \(c)\ is a constant
\(z=ζ+c^2ζ\)・・・(eq.3)
Using this equation, the center point in the \((ζ)\)-plane will become \((ξ_0,η_0)\), and the circle passing through point \((c,0)\) is transformed to an airfoil shape in the \(z)\-plane.
The 2 variables included in the coordinates of \((ζ)\)-plane, \((ξ_0)\)represents the thickness of an airfoil, and \(η_0)\) represents the curvature.
Substitute (eq.1) and (eq.2) into (eq.3) to divide real numbers and imaginary numbers.
You’ll derive 2 equations (eq.4) and (eq.5).
\(x=ξ+(c^2ξ/(ξ^2+η^2))\)・・・(eq.4)
\(y=η-(c^2η/(ξ^2+η^2))\)・・・(eq.5)
The Joukowsky airfoil appears by connecting the points \((x,y)\) calculated by substituting the coordinate points on the circumference passing through the point \((c,0)\) for \((ξ,η)\) in (eq.4) and (eq.5).